우선순위 큐
우선순위 큐란?
일반적인 큐(FIFO)와 달리 우선순위가 높은 데이터가 먼저 나가는 자료구조
구현방법
| 삽입 | 삭제 | |
| 배열 | O(1) | O(N) |
| 링크드리스트 | O(1) | O(N) |
| 힙 | O(logN) | O(logN) |
⏩️ 우선순위 큐의 삽입, 삭제가 필요할 때는 힙으로 구현하자.
최소 힙
- 이진트리 구조
- 모든 부모 노드는 자식 노드보다 값이 작다
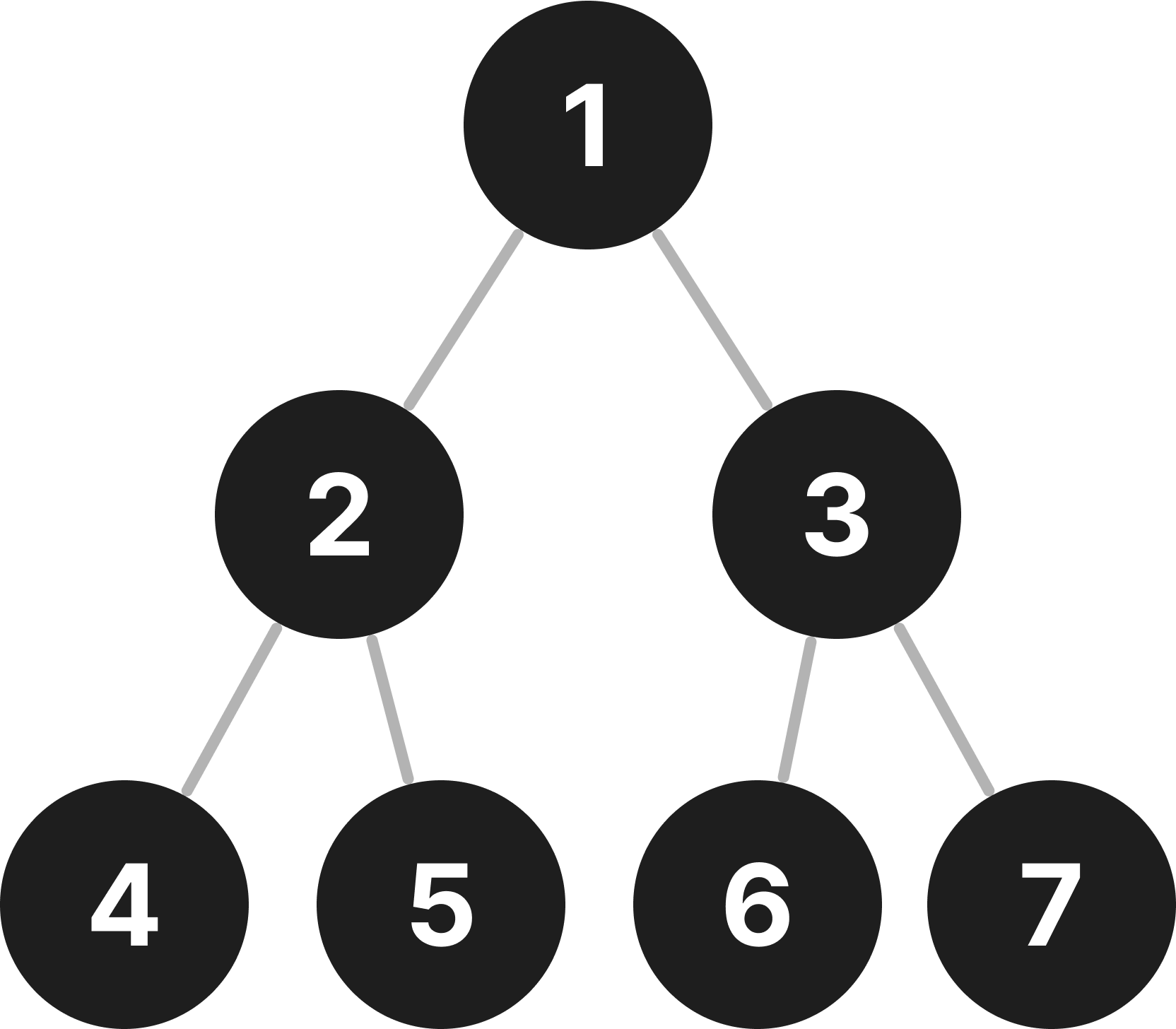
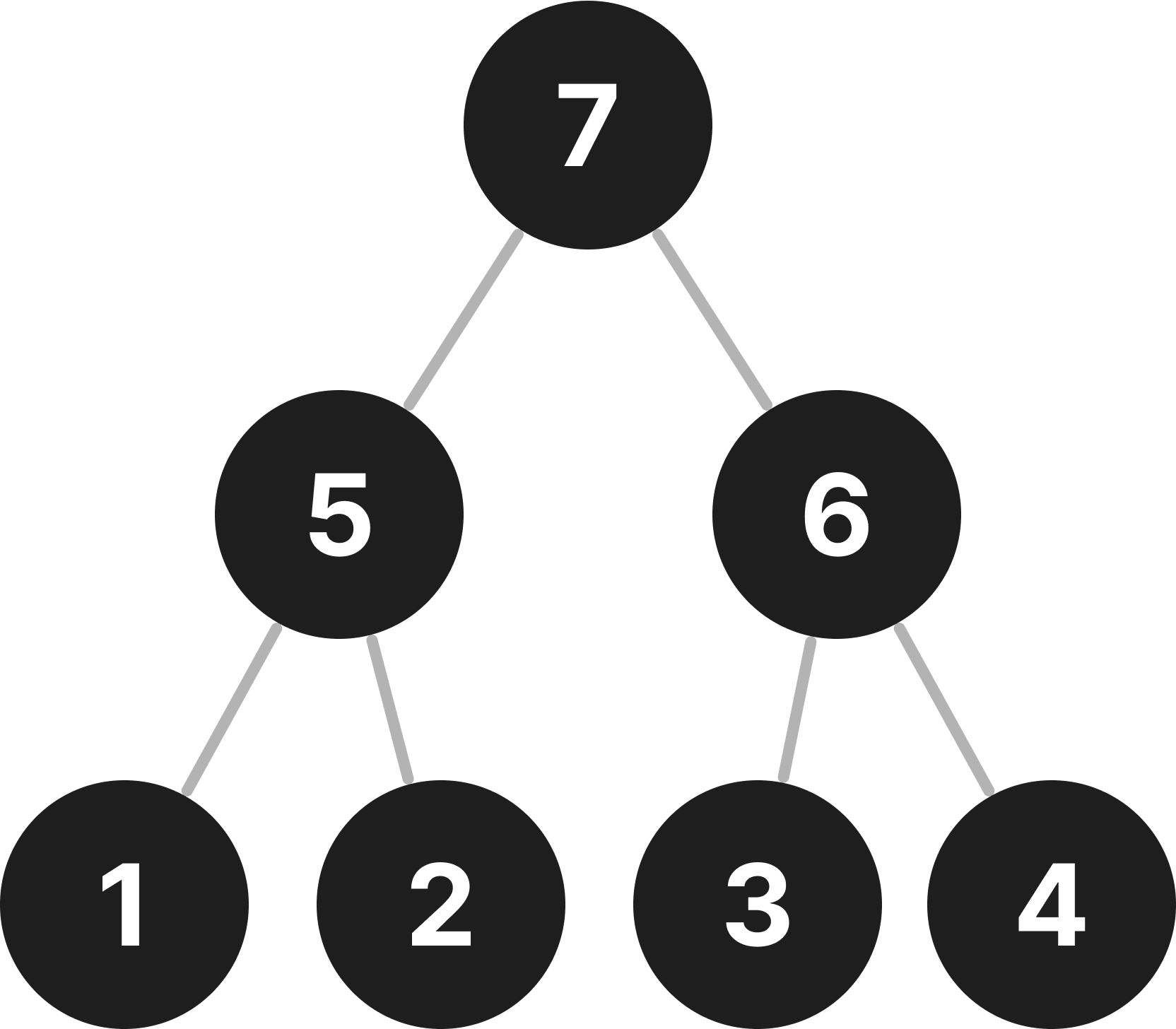
최대 힙
- 이진트리 구조
- 모든 부모 노드는 자식 노드보다 값이 크다
비겁하지만...
힙이 JS에는 구현이 안되어 있어서 직접 구현해야 한다.
코딩테스트에서 파이썬 사용이 가능하다면 파이썬으로 푸는게 더 유리하다.
파이썬에서는요
import heapq
# 힙 배열로 선언
heap = []
# 원소 push
heapq.heappush(heap, 1)
# 원소 pop
cur = heapq.heappop(heap)사실상 import heapq 하나로 끝
- 최소 힙 - 파이썬의 기본 heapq의 구현 (루트 노드가 최솟값)
- 최대 힙 - push할 때 값에 -를 붙여서 넣어주면 된다. (루트 노드에 -를 다시 붙이면 최댓값)
- 예를 들어 [1, 2, 3, 4, 5] 가 있다면 힙에 -를 붙여 넣었을 때,
- -5가 최솟값이므로 가장 루트 노드로 들어갈 것이다.
- 여기에 다시 -를 붙이면 최댓값 5를 얻을 수 있다.
그래도 굳이굳이 JS로 구현하자면
JS도 마찬가지로 최소 힙 하나만 구현하면 최대 힙도 사용할 수 있다.
힙은 배열로 구현한다.
구현하기 전에 알아야 할 것
- 왼쪽 자식 인덱스 = 부모 인덱스 * 2
- 오른쪽 자식 인덱스 = 부모 인덱스 * 2 + 1
- 부모 인덱스 = Math.floor(자식 인덱스 / 2)
- 위 인덱스들은 1부터 시작했을때 기준
삽입
- 힙의 가장 마지막에 삽입 값 push
- 삽입한 노드와 부모 노드 비교, 부모 노드보다 삽입한 노드가 더 작다면 swap
삭제
- 루트 노드와 가장 끝 노드 swap
- 가장 끝 노드 pop
- 루트 노드부터 비교 시작. 부모 노드가 자식 노드보다 더 크면 swap
- 왼쪽 자식 노드와 오른쪽 자식 노드 중 더 값이 작은 노드 찾기
- 자식 노드 중 작은 노드와 부모 노드 비교
구현
class MinHeap {
constructor() {
this.heap = [null];
}
#swap(a, b) {
[this.heap[a], this.heap[b]] = [this.heap[b], this.heap[a]];
}
size() {
return this.heap.length - 1;
}
heap_push(value) {
// 1. 가장 마지막에 push
this.heap.push(value);
// 2. 부모노드와 비교하며 작다면 부모노드와 swap
let curIdx = this.size();
let parentIdx = Math.floor(curIdx / 2);
while (this.heap[curIdx] < this.heap[parentIdx]) {
this.#swap(curIdx, parentIdx);
curIdx = parentIdx;
parentIdx = Math.floor(curIdx / 2);
}
}
heap_pop() {
if (!this.size()) {
return null;
}
if (this.size() === 1) {
return this.heap.pop();
}
// 1. 가장 끝 노드와 swap
this.#swap(1, this.size());
// 2. 가장 끝 노드 없애기
const value = this.heap.pop();
// 3. 왼쪽 / 오른쪽 자식과 비교 후 현재 노드가 더 크면 swap
let curIdx = 1;
let leftChildIdx = curIdx * 2;
let rightChildIdx = curIdx * 2 + 1;
while (
(this.heap[leftChildIdx] &&
this.heap[curIdx] > this.heap[leftChildIdx]) ||
(this.heap[rightChildIdx] && this.heap[curIdx] > this.heap[rightChildIdx])
) {
// 3-1. 왼쪽과 오른쪽 자식 중 더 작은 값의 인덱스 찾기
const smallIdx =
this.heap[rightChildIdx] &&
this.heap[leftChildIdx] > this.heap[rightChildIdx]
? rightChildIdx
: leftChildIdx;
// 3-2. 비교 후 현재 인덱스의 값이 더 크면 swap
if (this.heap[curIdx] > this.heap[smallIdx]) {
this.#swap(curIdx, smallIdx);
curIdx = smallIdx;
}
leftChildIdx = curIdx * 2;
rightChildIdx = curIdx * 2 + 1;
}
return value;
}
top() {
if (!this.size()) {
return null;
}
return this.heap[1];
}
}
🤮 그래도 시간이 많은 상황이면 직접 구현하자.
'알고리즘 > 자료구조' 카테고리의 다른 글
| [JS] 자바스크립트 스택 구현하기 (0) | 2024.02.01 |
|---|---|
| [JS] 자바스크립트에는 내장 라이브러리에 큐가 없는데 어떡하지 (2) | 2024.01.11 |
