0. 행렬 곱셈 방법
아이패드 있을때 추가하기..
n * m 행렬과 m* k 행렬의 곱!
1. General Solution
1.1 브루트포스
# 일반적인 3중 반복문 행렬 곱셈
answer = [[0 for _ in range(k)] for _ in range(n)]
for f in range(n):
for s in range(k):
for j in range(m):
answer[f][s] += a[f][j] * b[j][s]1️⃣ n번 반복하면서 첫번째 행렬의 행을 순회한다
2️⃣ k번 반복하면서 두번째 행렬의 열을 순회한다
3️⃣ m번 반복하면서 곱셈을 진행한다
➡️
1.2 분할정복
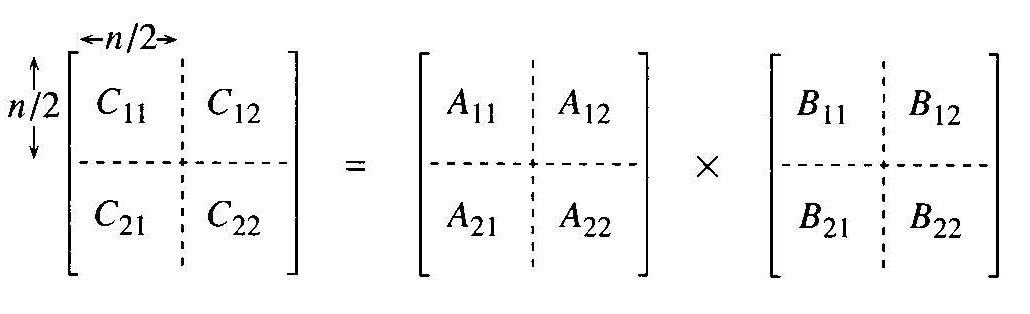
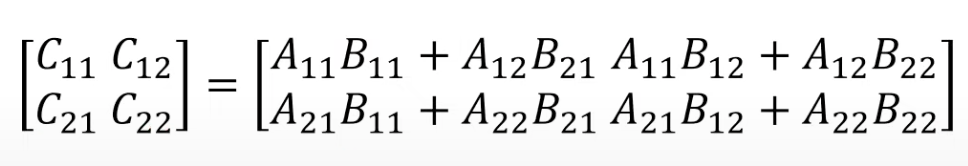
8번의 곱셈이 필요하다
8번의 덧셈이 필요하다
➡️ Θ(n^3)의 시간복잡도를 가진다
2. Strassen
(정방 행렬의 경우)
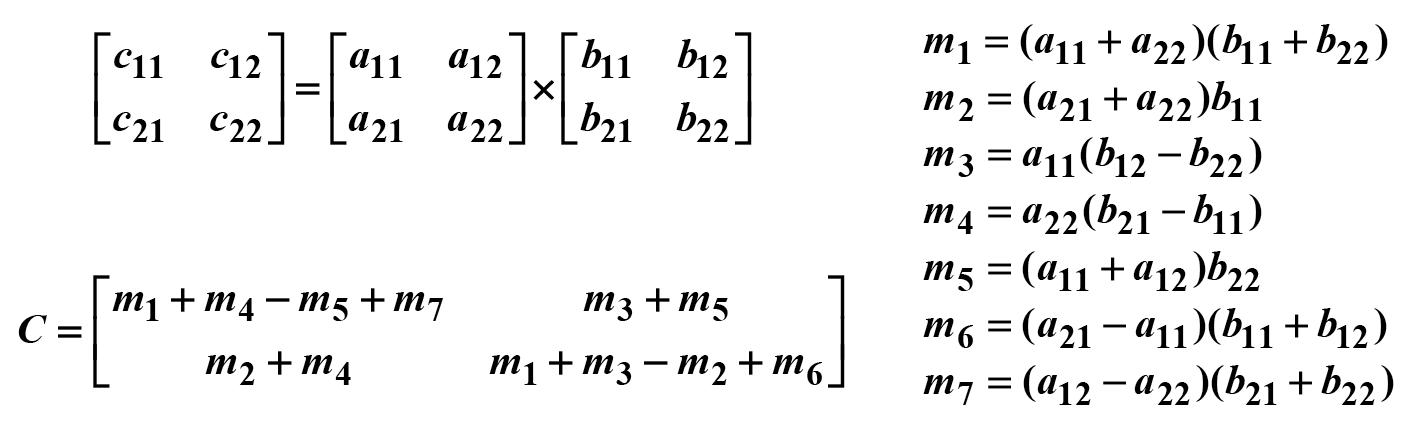
7번의 곱셈이 필요하다
18번의 덧셈이 필요하다
➡️ Θ(n^2)의 시간복잡도를 가진다
어려운 개념인 줄 알았는데 결국 분할정복을 거쳐 슈트라센 연산이 가능한 형태로 만들어야 사용할 수 있고, m1~m7의 값을 다 저장해야 하기 때문에 잘 안쓰이는 것 같다...
📝 체크포인트
- 분할정복 수도코드
- 시간복잡도 비교
백준 2740 10830
'알고리즘 > 알고리즘 개념' 카테고리의 다른 글
| BFS (0) | 2023.04.11 |
|---|---|
| 이분탐색 (0) | 2023.04.11 |
| 이항계수 (+페르마의 소정리) (0) | 2023.04.11 |
| 플로이드 워셜 알고리즘 (0) | 2023.04.11 |
| 유클리드 호제법 (1) | 2023.03.28 |
