0. 이항계수란
- n개 중 k개를 뽑는 조합의 수
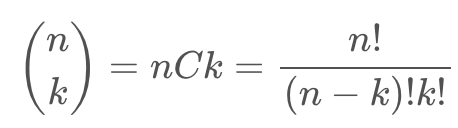
- 이항계수의 성질
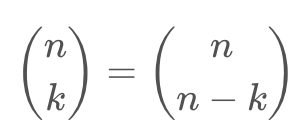
1. n개 중에 k개를 뽑는 것과 n개 중에 n-k개를 뽑는 경우의 수는 같다
(뽑지 않을 것을 정하는 것과 뽑을 것을 정하는 것은 같다)
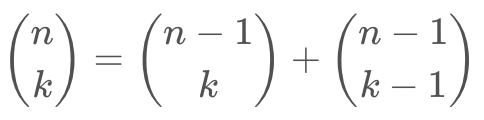
2. n-1개 중에 k개를 뽑는 경우의 수와(1개 포함X) n-1개 중에 k-1개를 뽑는 경우의 수(1개 포함O)를 더하면
n개 중에 k개를 뽑는 경우의 수이다
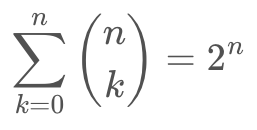
3. nC0부터 nCn까지의 합은 2^n 이다
1. 분할정복을 이용한 이항계수 구하기
1.1 알고리즘 진행과정
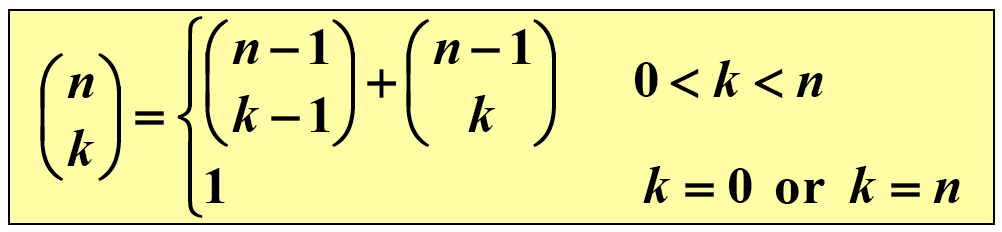
0️⃣ nC0 혹은 nCn 은 항상 1이다
1️⃣ 나머지 경우는 이항계수의 2번 성질을 활용하여 구현
시간복잡도가 O(n!)이라서 엄청나게 비효율적..
1.2 코드
def bino(n, k):
if k == 0 or n == k:
return 1
else:
return bino(n-1, k-1)+bino(n-1, k)2. DP를 이용한 이항계수 구하기
2.1 알고리즘 진행과정
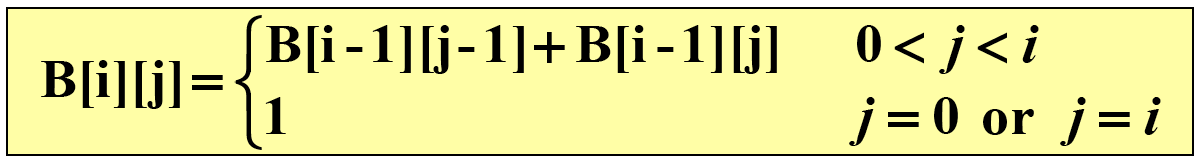
0️⃣ n과 k를 순회하면서! nC0 혹은 nCn인 경우 1 저장
1️⃣ 나머지 경우는 이항계수의 2번 성질을 활용하여 저장
시간복잡도 O(N^2)
2.2 점화식
memo[i][j] = memo[i-1][j-1] + memo[i-1][j]
2.3 코드
for i in range(1, n+1):
for j in range(k+1):
if i == j or j == 0:
memo[i][j] = 1
else:
memo[i][j] = memo[i-1][j-1]+memo[i-1][j]
3. 페르마의 소정리를 이용한 이항계수 구하기
3.0 페르마의 소정리란
![]()
a는 정수, p는 소수
a의 p승을 p로 나눈 나머지는 a를 p로 나눈 나머지와 같다
양변을 a로 나누면
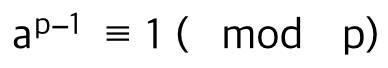
3.1 알고리즘 진행과정
좀더 고민해보자.. (DP가 어디 범위까지 될지도 생각해보기)
